Weibull分布中的形状参数β值，有什么意义？

　　使用Weibull++进行寿命数据分析

　　在目前可靠性分析中，Weibull分布是最广泛应用的一个概率分布。

　　Weibull分布的两个参数β(BETA)和η(ETA)也各有其含义。许多可靠性工程师一直恐惧看到大数值的形状参数β。

　　但大数值β其实并不是一件坏事。

　　Weibull分布和形状参数β

　　Weibull模型最初是在20世纪中叶由Waloddi Weibull引入的，由于其良好的灵活性而被广泛应用。该分布的形状参数，通常表示为希腊字母β。

　　对于所分析的数据，该参数所代表的意义是相当有描述性的。

　　例如，β的值描述了故障率随时间变化的趋势。小于1的β值表明，故障率随着时间的推移而下降，通常与“早夭”或早期发生的缺陷故障有关。β值约等于1表示故障率不随时间变化，故障时间具有随机性。大于1的β值表明，故障率随着时间的推移而增加，通常与机械磨损疲劳相关的故障有关。

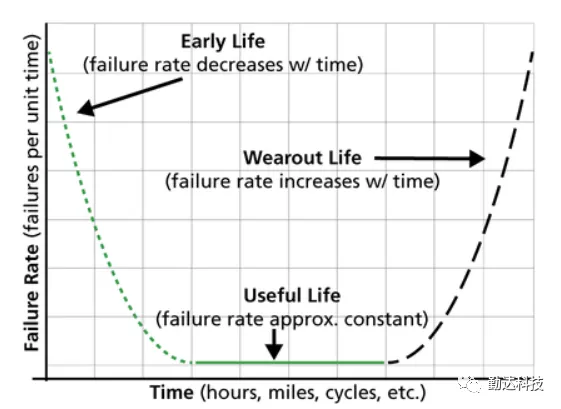
　　对于机械产品的寿命数据进行可靠性分析，得出β值大于1的现象并不少见。

　　然而，当β的计算值远大于1（例如，6或更大）时，有些可靠性工程师可能会不知道如何解释这一现象。这样高的测试值有时被认为是产品或测试在某种程度上存在缺陷的迹象。 然而这种现象经常存在于机械零部件的测试中。

　　Weibull本人在他1951年的论文《A statistical distribution function of wide applicability》中也发表了一组ST-37钢的疲劳数据，β值是5.956.

　　高β值的例子

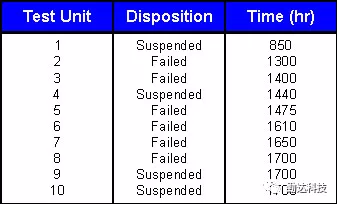
　　一位工程师正在考虑一个小型真空泵的设计，该真空泵将被纳入一个更大的系统之中。 系统的可靠性分配要求真空泵在1000小时内必须具有95%的可靠性，90%的置信度才能达到系统的目标。工程师从一个可能的供应商那里获得10个真空泵的样本，并将它们置于寿命测试之下，以确定特定的泵设计是否符合规范。

　　本次寿命试验结果见下表：

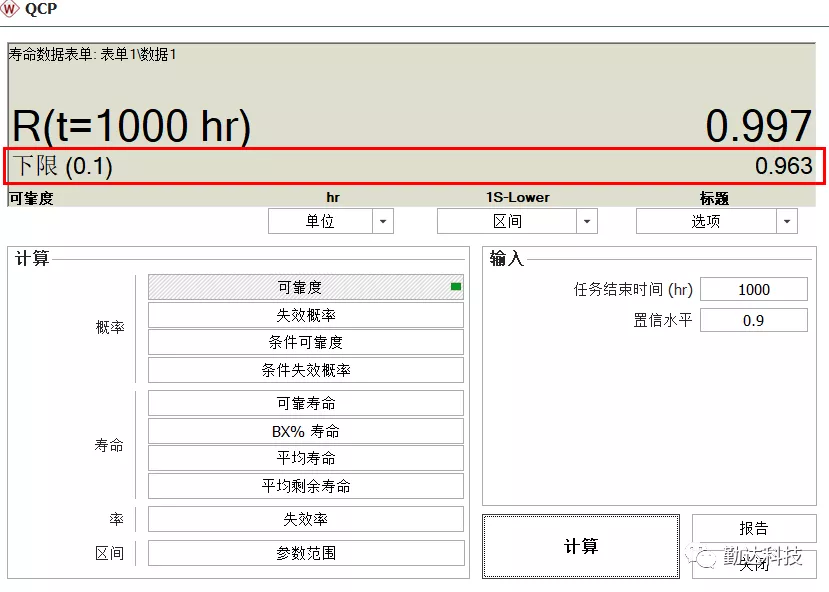
　　通过ReliaSoft的Weibull++软件，采用极大似然估计(MLE)分析方法，工程师估计数据的Weibull参数为η=1665.5小时，β=11.6。

　　这可能会让工程师感到震惊，因为11.6的β值相对较高。

　　然而，当他持续进行分析，工程师发现在1000小时，90%的置信度时，可靠性估计为96.3%。这个结果满足可靠性为95%的规范。

　　尽管β值很高，但测试或产品并没有任何问题！

　　如何解释高β值？

　　Weibull形状参数是衡量数据分布变异性的指标，高β值意味着低变异性。

　　因此，如果测试样本具有较高的β值，则表明这些样本所代表的weibull故障分布较为集中，将在较小的时间范围内失效。反之，如果β值小，则代表发生故障时间的范围大，不确定性更大。

　　换句话说

　　形状参数（β）的高值本身并不是问题，只要尺度参数的相应值(η)足够高，就可以使产品达到可接受的整体可靠性要求。

　　同时较高的β值也意味着产品材料的均匀程度较高，设计也相对稳定且同质或者是测试产品从同一批次生产，变异性相对较低。

　　事实上，对于可修复系统，具有高β值的零部件实际上可能是首选的。

　　因为变异性小可以提高预防性维护程序的效率。更少的变异性意味着故障以更“受控”的方式发生，因此可以量化预防性维修的最佳更换间隔。

　　例如，对于预防性维护程序来说，最好有一个零部件，它总是在精确的1000小时运行时失效。因此，最佳更换时间将在预期故障之前，即999.9小时。

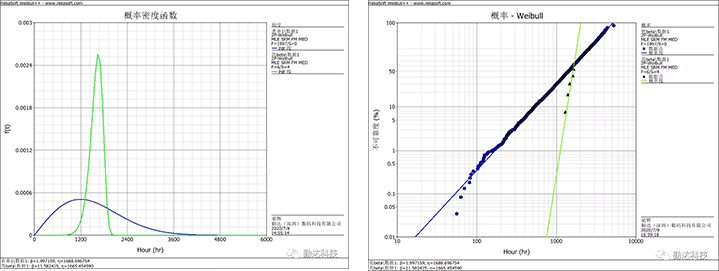
　　与具有较高β值相关的另一个关注点是，概率图中相对陡峭的斜率使得工程师很难识别数据中的存在规律，例如存在异常值或数据的拐点。

　　其实通过查看概率图中的模式，可以识别出的大多数问题有望在工程和测试过程中被检测到。

　　例如，数据模式中的拐点可能是由于存在多种故障模式或者故障机理。虽然概率图上的陡坡可能会掩盖这一拐点，但在测试过程中或故障分析中可能会观察到多种故障模式的存在。

　　ReliaSoft的Weibull++软件就可以通过混合weibull分布来分辨数据中的不同失效模式。

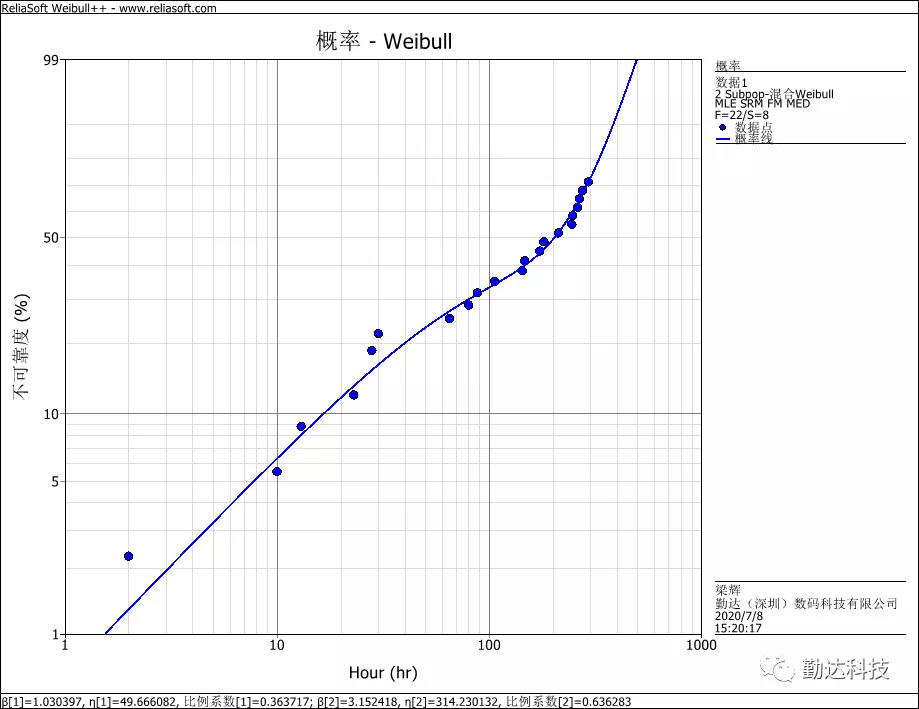
　　混合weibull：两种失效模式（概率图中存在拐点）

　　通过上面的分析，我们知道，

　　对于具有较高β值的数据，需要先确定测试的方法不存在问题，同时产品没有批次性问题，那么只要η值足够高，产品的测试结果能否符合最终设计要求才是需要关注的地方。